Chebyshev iteration

If we know an interval containing the eigenvalues, it is possible to design a scheme with near optimal convergence.

Let’s start with a splitting-style approach:

$$\begin{array}{c}A=M-N\\ x^{(k+1)}=M^{-1}(b+N{x}^{(k)})\\ x^{(k+1)}=M^{-1}(b+(M-A)x^{(k)})\end{array}$$

This implies that

$$x^{(k+1)}=x^{(k)}+M^{-1}(b-A{x}^{(k)})$$

This is the residual iteration form.

Let’s avoid repeating $M^{-1}$ in all the equations and let’s do the substitution:

$$M^{-1}b\to b,M^{-1}A\to A.$$

Then the iteration is:

$$x^{(k+1)}=x^{(k)}+b-A{x}^{(k)}$$

This substitution can also be interpreted as solving $M^{-1}Ax=M^{-1}b$ instead of $Ax=b$.

Let’s apply our idea of relaxation:

$$x^{(k+1)}=x^{(k)}+{\omega }_k(b-A{x}^{(k)})$$

Let’s use the equality $x=x+{\omega }_k(b-Ax)$, and subtract:

$$\begin{array}{c}{e}^{(k)}=x^{(k)}-x\\ e^{(k+1)}=(I-{\omega }_{k}A)e^{(k)}\end{array}$$

We get:

$$\begin{array}{c}{e}^{(k+1)}=(I-{\omega }_{k}A)\cdots (I-{\omega }_{0}A)e^{(0)}\\ e^{(k)}=p_k(A)e^{(0)}\end{array}$$

where $p_k$ is a polynomial of order $k$ with $p_k(0)=1$.

Note: there is a variant where we use

$$x^{(k+1)}=x^{(k)}+{\omega }_k(b-A{x}^{(k)})-{\alpha }_k(x^{(k)}-x^{(k-1)})$$

Then:

$$e^{(k+1)}=((1-{\alpha }_k)I-{\omega }_{k}A)e^{(k)}+{\alpha }_k{e}^{(k-1)}$$

In both cases: $e^{(k)}=p_k(A)e^{(0)}$ with $p_k(0)=1.$

The polynomial $p_k$ needs to be designed to provide maximum error reduction. Estimating $p_k$ requires having an estimate of an interval containing the eigenvalues of $A.$

Assume that the eigenvalues of $A$ are in the interval $[m,M]$.

Then define the following polynomial:

$$p_k(x)=\frac{T_k(z(x))}{T_k(z(0))}$$

where $T_k$ is a Chebyshev polynomial. Here we also used a shift-and-scale transformation of $x$:

$$z(x)=\frac{m+M-2x}{M-m}$$

We have $p_k(0)=1$. Moreover when $m\le x\le M$:

$$\begin{array}{c}2m\le 2x\le 2M\\ -2M\le -2x\le -2m\\ m-M\le m+M-2x\le M-m\\ -1\le z(x)\le 1\end{array}$$

So $|T_k(z(x))|\le 1$ and

$$\begin{array}{c}|p_k(x)|\le \frac{1}{|T_k(z(0))|}\\ z(0)=\frac{M+m}{M-m}=1+\frac{2m}{M-m}>1\end{array}$$

So as before $|T_k(z(0))|\gg 1$ and $|p_k(x)|\ll 1$ for $m\le x\le M.$

We can prove the following bound:

$$\begin{array}{c}\Vert e^{(k)}{\Vert }_2\le \Vert p_k(A){\Vert }_2\Vert e^{(0)}{\Vert }_2\\ \Vert p_k(A){\Vert }_2\le \Vert X{\Vert }_2\Vert X^{-1}{\Vert }_2\Vert \Lambda {\Vert }_2\le \kappa (X)\underset{x\in [m,M]}{\max }|p_k(x)|\end{array}$$

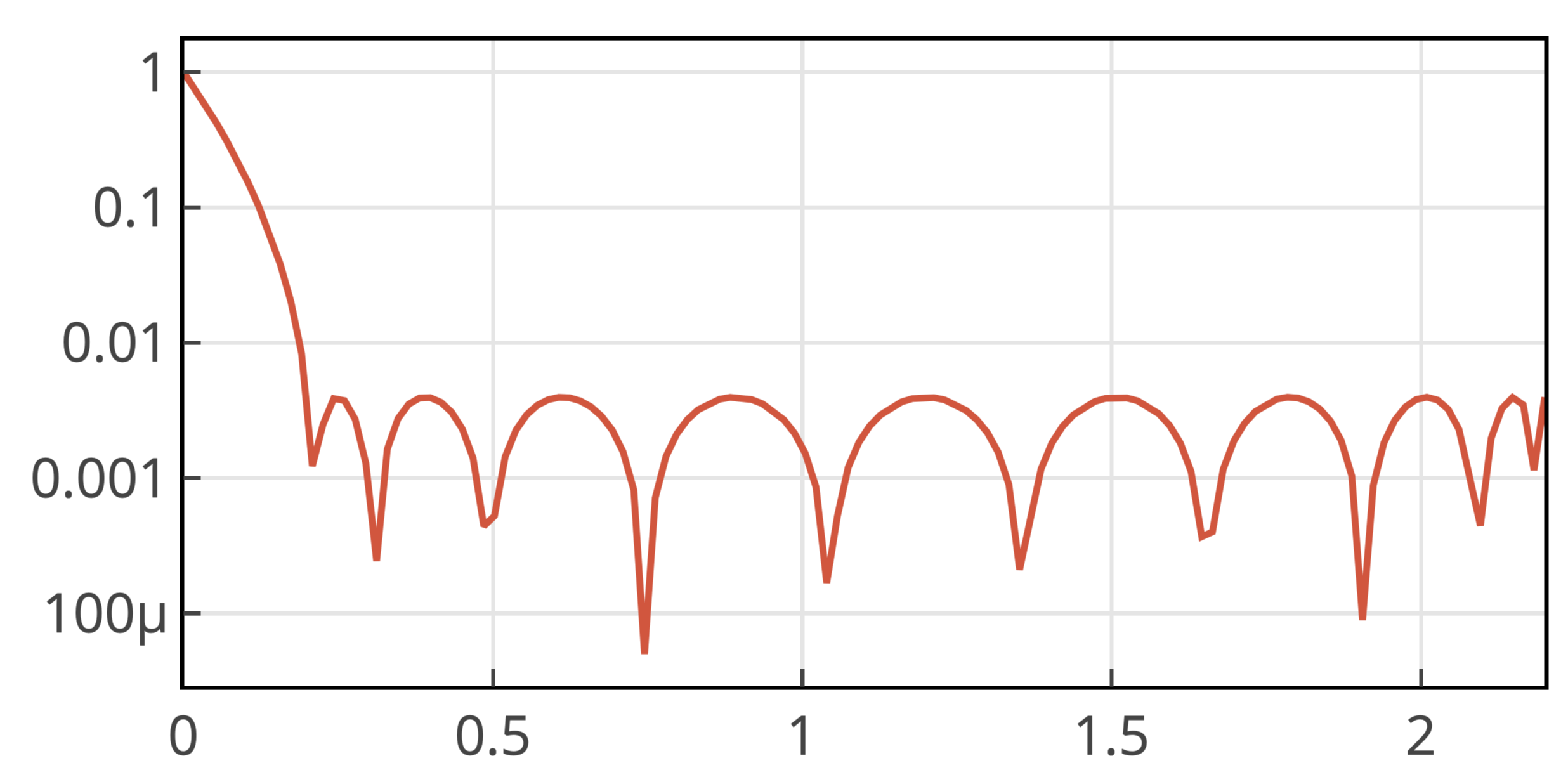
We can expect a rapid convergence. But this algorithm requires a good estimation of $m$ and $M$.

We can derive a more precise bound for

$$\underset{x\in [m,M]}{\max }|p_k(x)|$$

We have for $|z|>1$:

$$T_n(z)=\frac{1}{2}[(z+\sqrt{z^2-1}{)}^n+(z-\sqrt{z^2-1}{)}^n]$$

where

$$z=\frac{M+m}{M-m}$$

Denote by $u$

$$u=\frac{m}{M}$$

Then using $a^2-b^2=(a-b)(a+b)$:

$$\begin{array}{rl}z+\sqrt{z^2-1}& =\frac{1+u}{1-u}+\sqrt{(\frac{1+u}{1-u}{)}^2-1}\\ & =\frac{1+u+2\sqrt{u}}{1-u}=\frac{(1+\sqrt{u}{)}^2}{(1-\sqrt{u})(1+\sqrt{u})}\\ & =\frac{1+\sqrt{u}}{1-\sqrt{u}}\end{array}$$

Moreover:

$$z-\sqrt{z^2-1}=\frac{1}{z+\sqrt{z^2-1}}$$

Finally:

$$\underset{x\in [m,M]}{\max }|p_k(x)|\le \frac{1}{|T_n(z)|}=\frac{2}{{\tau }^{-n}+{\tau }^n}=\frac{2{\tau }^n}{1+{\tau }^{2n}}$$

with

$$\tau =\frac{1-\sqrt{u}}{1+\sqrt{u}}$$

This expression can be simplified. Assume that the interval containing the eigenvalues is small: $m<M$ and $m\to M$. Then $u\to 1$ and $\tau \to 0$. We get:

$$\underset{x\in [m,M]}{\max }|p_k(x)|\le \frac{1}{|T_n(z)|}\le 2{\tau }^n\le 2(1-\sqrt{\frac{m}{M}}{)}^n$$

The convergence is very fast. The figure below shows the polynomial with $m=0.2$ and $M=2.2$.