Least-squares solution using SVD

What if $A$ is not full column rank?

$$A=QR$$

• The QR factorization exists but is not unique.
• $R$ is singular.
• So:

$$x=R^{-1}{Q}^{T}b\to \text{fails}$$

The problem is that the solution of the least-squares problem is non-unique.

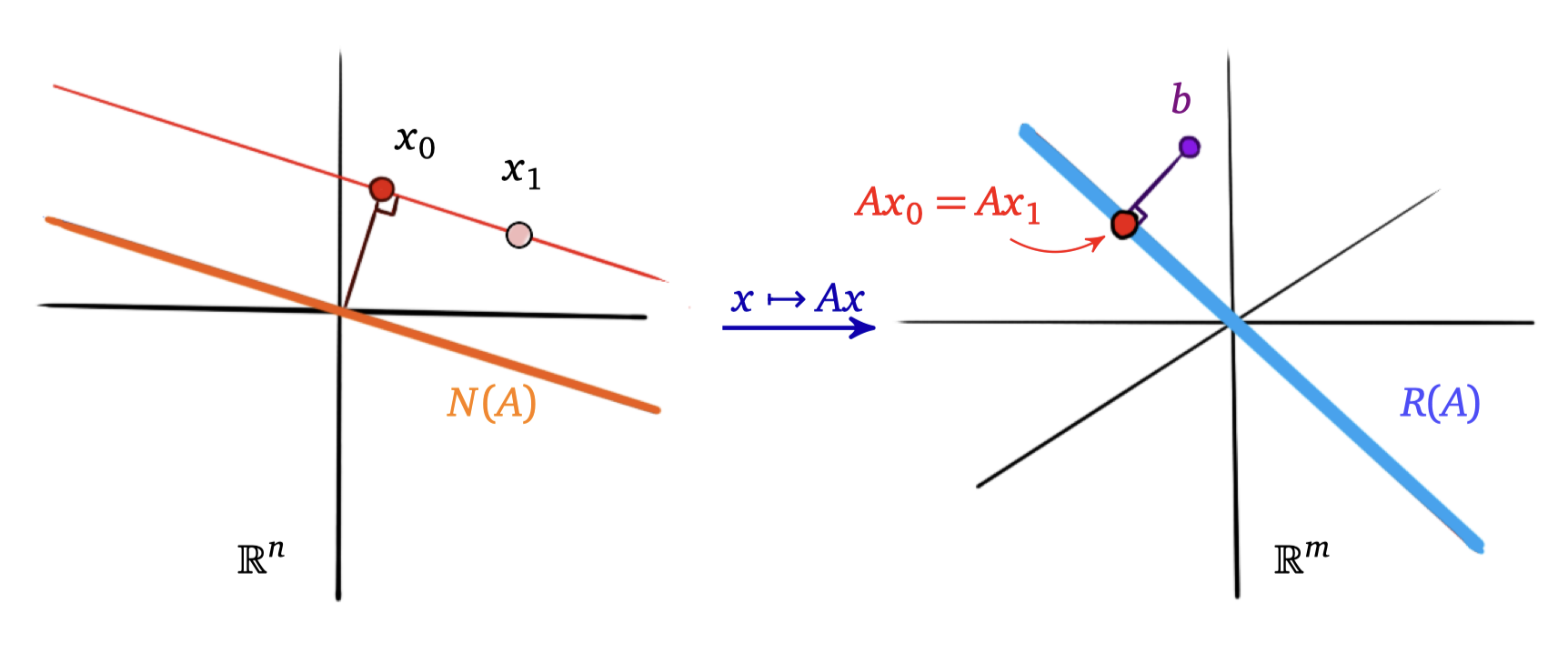
• We need to look for the solution with minimum norm.
• This solution is unique.
• It satisfies two conditions:

1. ${\text{argmin}}_x\Vert Ax-b{\Vert }_2$: it solves the least-squares problem.
2. $x\perp N(A)$, that is, the solution has a minimum 2-norm.

Here are the solution steps.

Let’s start with the thin SVD:

$$A=U\Sigma V^T$$

Shape of matrices:

• Because $A$ is not full column rank, we have that the rank $r$ satisfies $r<n$.
• This is why matrix $V$ is thin. $V$ and $U$ both have $r$ columns. $U$ has $m$ rows and $V$ has $n$ rows. $\Sigma$ has size $r\times r$.

Let’s go back to the equation

$$A^T(Ax-b)=0$$

This is equivalent to:

$$U^T(Ax-b)=U^T(U\Sigma V^{T}x-b)=0$$

Since $U^{T}U=I_r$

$$\Sigma V^{T}x=U^{T}b$$

• But $V^{T}x$ does not uniquely define $x$.
• We need to add the condition that $x\perp N(A)$. This guarantees that $x$ has minimum 2-norm.
• From $A=U\Sigma V^T$:

$$x\perp N(A)\iff x\perp (\text{span}(V{)}^{\perp })\iff x\in \text{span}(V)$$

• Note that because $A$ is not full column rank, its null space $N(A)$ is non-trivial.
• As a result $V$ is a thin matrix and span($V$)${}^{\perp }$ is non-trivial as well.
• Let’s now search for the solution $y$:

$$x\in \text{span}(V)\iff x=Vy$$

• The solution is then

$$\Sigma V^{T}Vy=\Sigma y=U^{T}b$$

since $V^{T}V=I$.

• That system has a unique solution in $y$ because all the singular values ${\sigma }_i$, $1\le i\le r$, are non-zero.
• The final solution is therefore

$$x=V{\Sigma }^{-1}{U}^{T}b$$

The computational cost to calculate the SVD is $O(m{n}^2)$.

Summary

• Dimensionality reduction: By using the thin SVD, we’re effectively reducing the problem to a smaller subspace where $A$ behaves well (invertible scaling via $\Sigma$). This avoids issues that arise from attempting to invert a singular matrix directly.

• Orthogonal decomposition: The SVD provides an orthogonal basis for both the row and column spaces of $A$. By projecting $b$ onto the column space via $U^{T}b$, we’re capturing the component of $b$ that $A$ can “reach”.

• Decoupling the problem: The diagonal nature of $\Sigma$ means that each component of $y$ (and thus $x$) can be solved independently. This decoupling simplifies the problem from solving a potentially complex system of equations to handling straightforward, individual equations.

• Avoiding the null space: By ensuring $x$ is in the span of $V$ (i.e., $x\perp N(A)$), we eliminate any arbitrary components that could exist in the null space of $A$. This is essential for finding the minimum-norm solution.

In practical applications, especially when dealing with data that may be noisy or ill-conditioned, finding a stable and unique solution is critical. The SVD provides a robust framework for:

• Handling rank deficiency: Even when $A$ lacks full rank, the SVD allows us to work within the subspace where $A$ is effective.

• Numerical stability: By avoiding the inversion of $A^{T}A$ (which can be ill-conditioned or singular), we reduce numerical errors and improve the stability of our computations.

• Interpretability: The SVD not only helps in solving the least-squares problem but also offers insights into the underlying structure of $A$, such as its rank and the significance of its singular values.

Least-squares problems, Singular value decomposition, Method of normal equation, Least-squares solution using QR