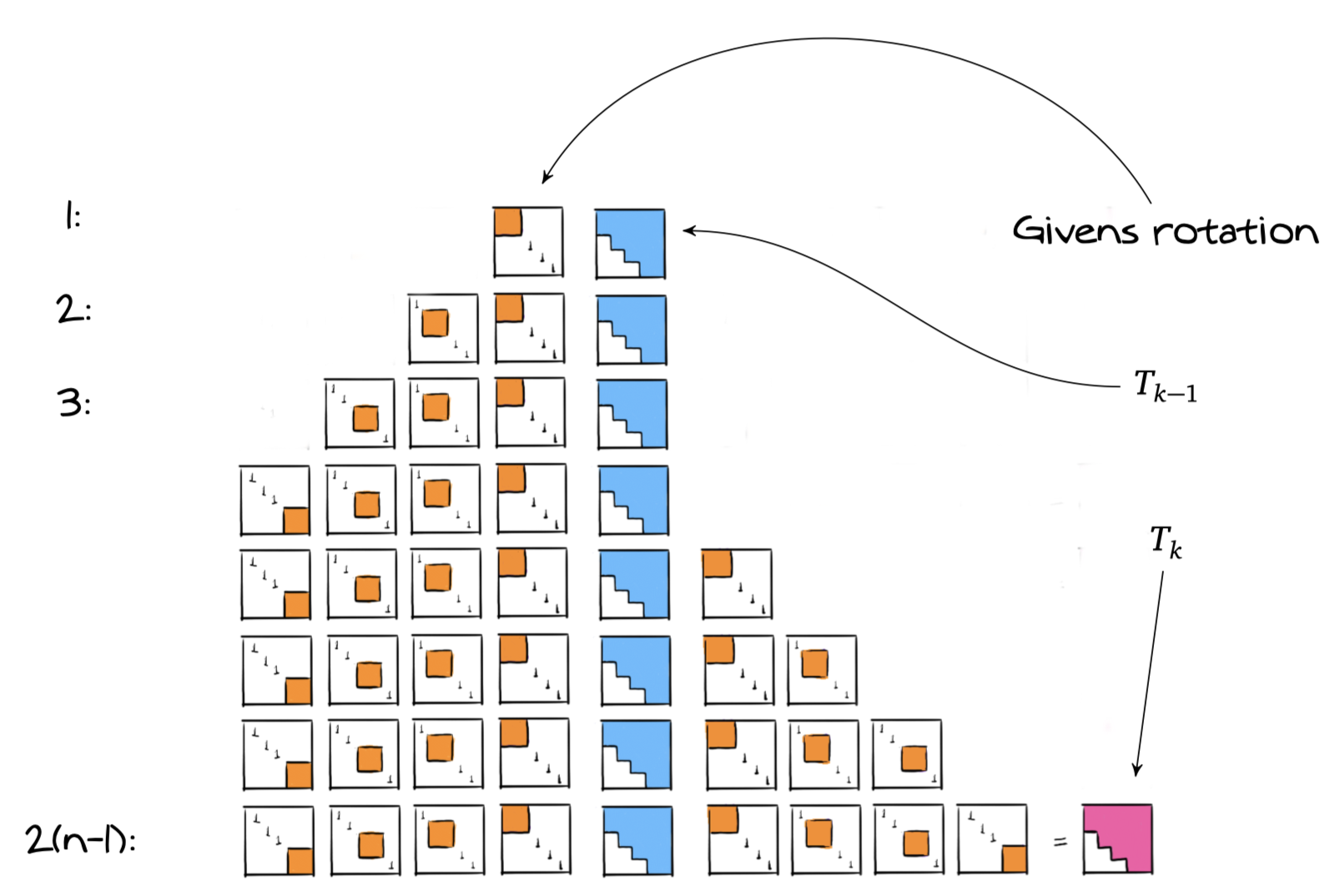
QR iteration for upper Hessenberg matrices

Let’s first perform a QR factorization step using Givens transformations.

Let’s do this step-by-step.

Step 1: We first perform a series of small Givens transformations applied to the left.

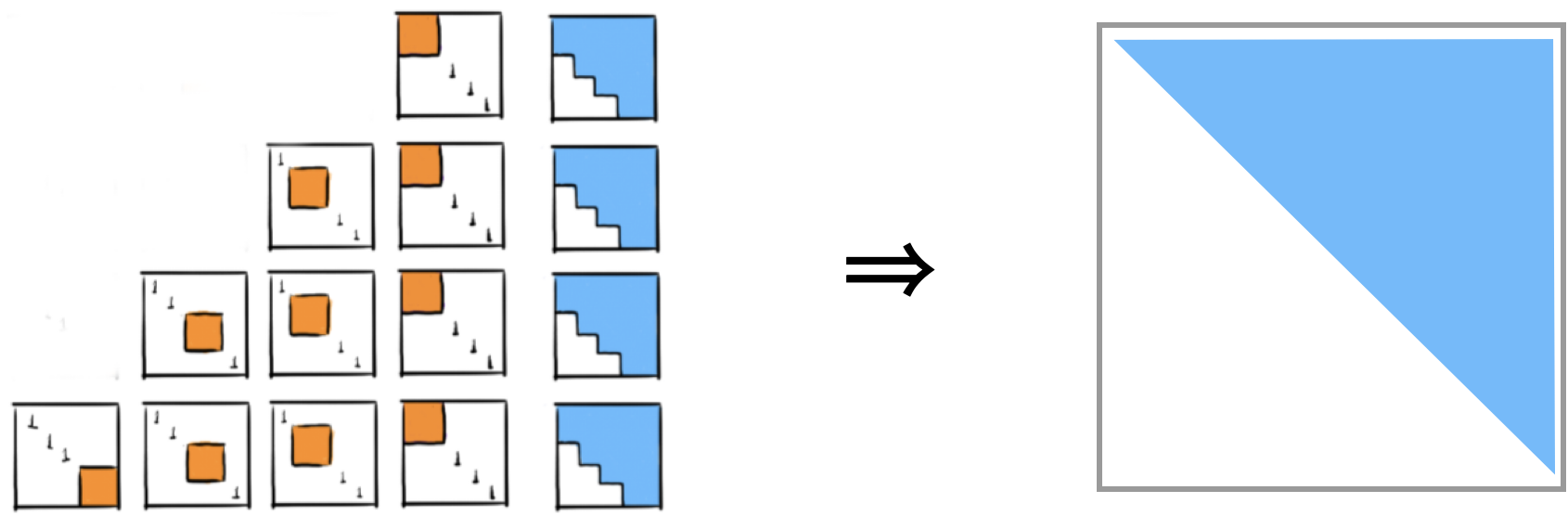
Step 2: Then these Givens transformations are applied to the right.

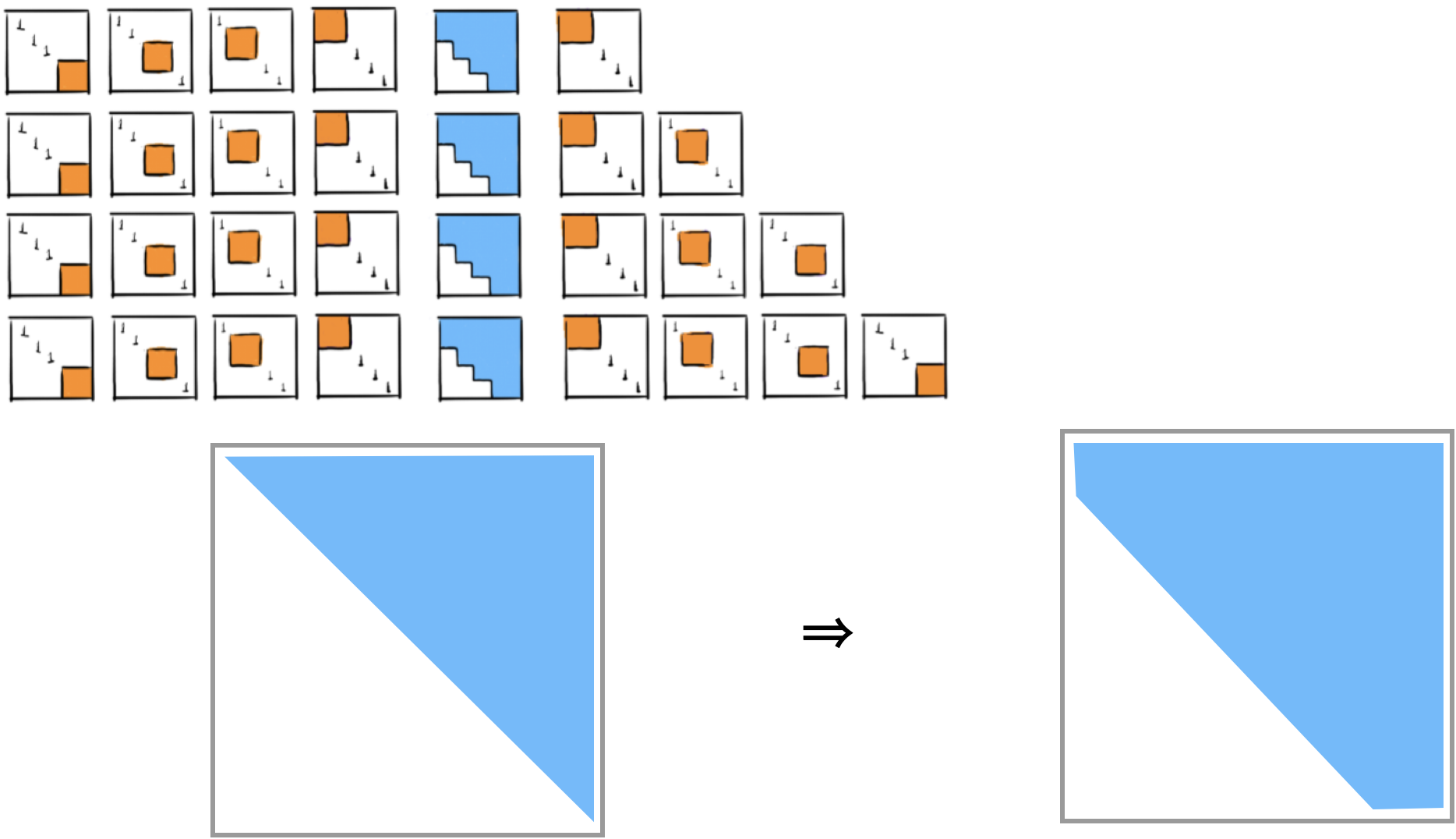
We obtain again a matrix in upper Hessenberg form.

Cost of QR: $O (n^{2})$
Cost of RQ: $O (n^{2})$
Total cost of one QR iteration: $O (n^{2})$

This is much less than the $O (n^{3})$ for the original QR iteration.

QR iteration with upper Hessenberg matrix

The QR iteration algorithm conserves the upper Hessenberg form.
The time cost per iteration in upper Hessenberg form is $O (n^{2})$ .
The total time cost is $O (n^{3})$ .

Geometric interpretation

Each QR step can be seen as a refined rotation of our coordinate system.
We are gradually aligning our axes with the eigenvectors, but doing so through a series of small, precise adjustments.
The Hessenberg form allows these adjustments to be made much more efficiently.

Algorithm:

function givens_QR_iteration_s!(H)
    n = size(H,1)
    G = zeros(2,n-1)
    for k=1:n-1
        c, s = givens(H[k,k], H[k+1,k])
        G[:,k] = [c; s]
        # Multiply by Givens rotation to the left
        apply_left_givens!(H, k, c, s)
    end
    for k=1:n-1
        # Multiply by Givens rotation to the right
        apply_right_givens!(H, k, G[1,k], G[2,k])
    end
end

Summary of one step of the QR iteration with the upper Hessenberg form