Upper Hessenberg form for the QR iteration

The key step becomes computing the QR factorization of $T_k$ and applying $U_k$ to the right of $R_k$.

This can be made more efficient if $A$ is in upper Hessenberg form:

We need a transformation of the form:

$$Q^{T}AQ=H$$

Note how $Q$ is applied to the left and right. This matrix is unitarily similar to $A$. The reason why this transformation is relatively easy to compute is the fact that $H$ is upper Hessenberg, instead of triangular as in the Schur decomposition.

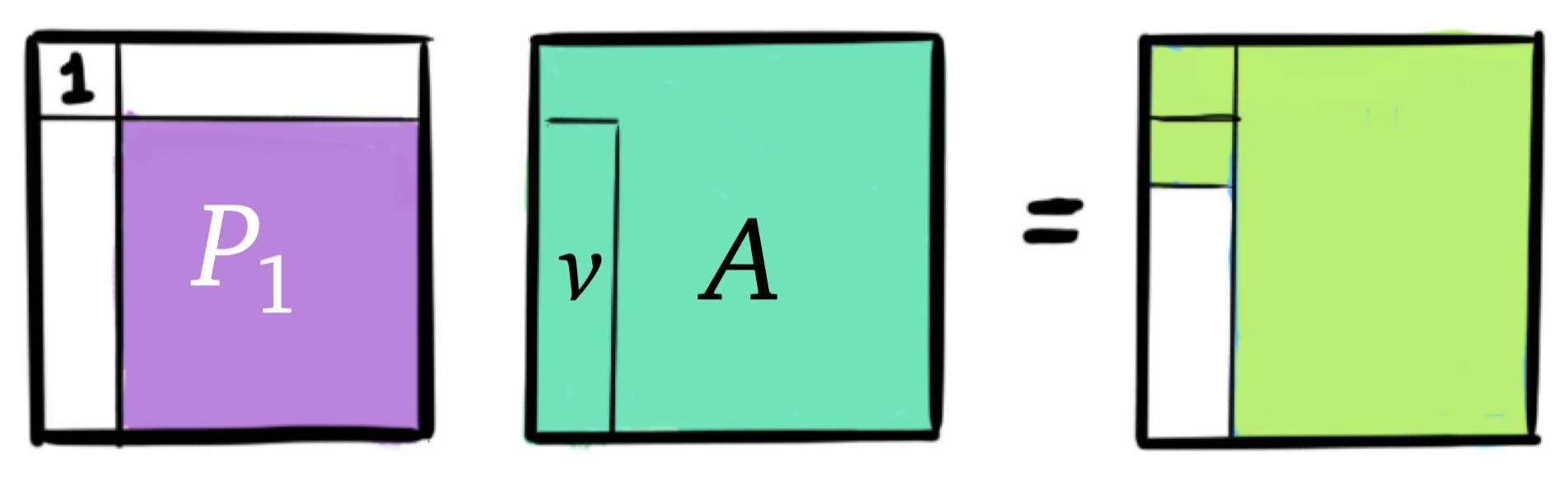
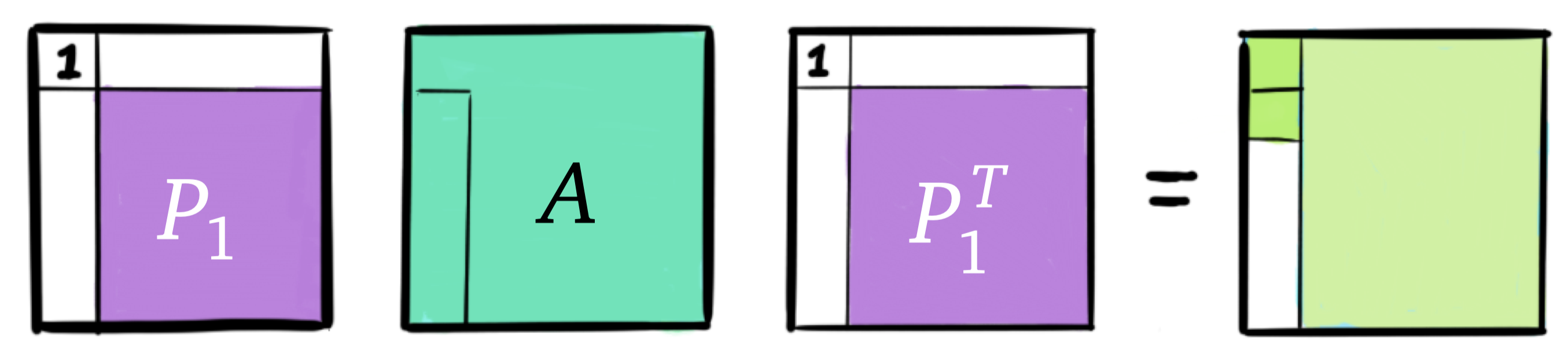
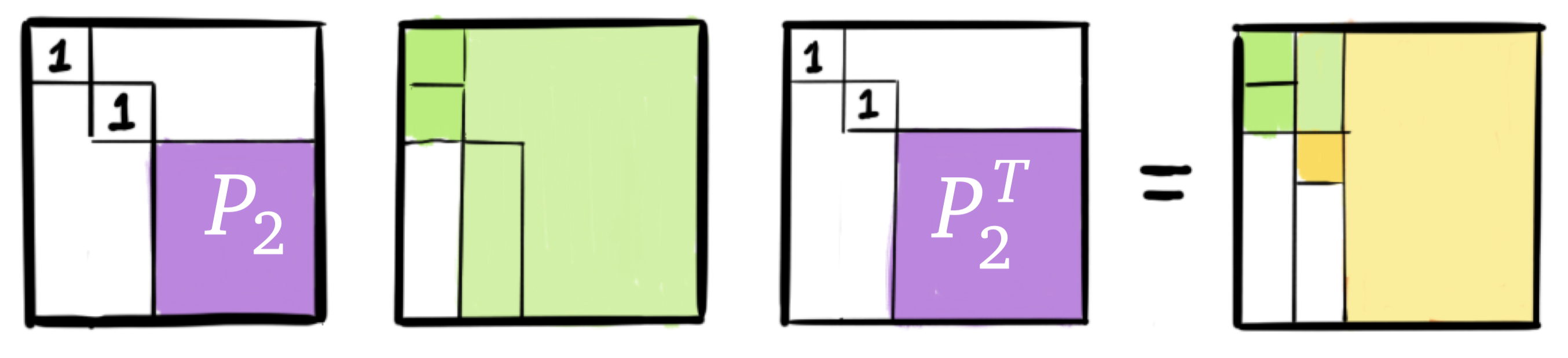
We can repeat this process until $A$ is in upper Hessenberg form. This process is similar to the QR factorization using Householder transformations. But note again that $Q$ is applied to the left and right so this is still a different process.

• Each orthogonal transformation costs $O(n^2).$
• The total computational cost is $O(n^3)$.
• This is very fast.
• Once this is done, the QR iteration becomes much faster.