Some orthogonality relations in CG

The name conjugate gradients comes from the fact that the search directions are orthogonal to each other with the right metrics. A special orthogonality relation needs to be used to prove this.

Definition. We say that two non-zero vectors $u$ and $v$ are $A$-conjugate with respect to $A$ if

$$u^{T}Av=0$$

Denote by

$$\Delta x^{(k)}=x^{(k+1)}-x^{(k)}.$$

Theorem. The solution increments $\Delta x^{(l)}$ and $\Delta x^{(k)},$ $l\ne k,$ are $A$-conjugate.

Proof.

$$(Q_k^{T}A{Q}_k)y_k=Q_k^{T}b\Rightarrow Q_k^T(b-A{x}^{(k)})=0.$$

This is a key result: the residual $b-A{x}^{(k)}$ is orthogonal to the Krylov subspace $\mathcal{K}(A,b,k)$.

Denote by $r^{(k)}=b-A{x}^{(k)}.$ Then we have that

$$\begin{array}{c}{Q}_k^T{r}^{(k)}=0\text{ and }{Q}_k^T{r}^{(k+1)}=0\\ \Delta x^{(k)}=x^{(k+1)}-x^{(k)}\\ A\Delta x^{(k)}=r^{(k)}-r^{(k+1)}\\ \Rightarrow Q_k^{T}A\Delta x^{(k)}=0\end{array}$$

But:

$$\begin{array}{c}\Delta x^{(l)}=x^{(l+1)}-x^{(l)}\in Q_{l+1}\\ \Rightarrow (\Delta x^{(l)}{)}^{T}A\Delta x^{(k)}=0,l<k\end{array}$$

$\square$

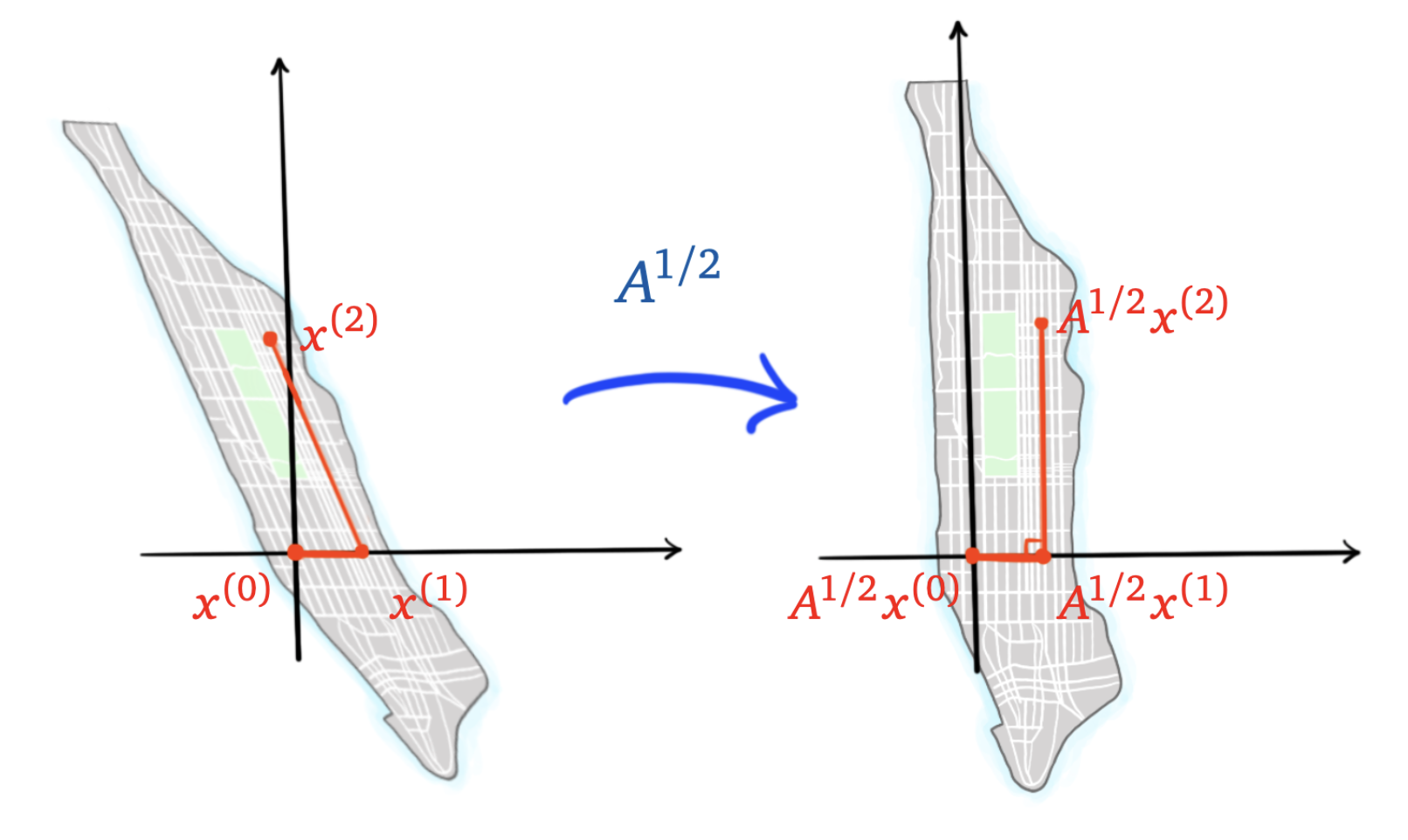
The steps in CG can be visualized as shown below. If we multiply the vectors by $A^{1/2}$ then each step is orthogonal to all the previous ones. This looks like a street map of Manhattan!