Convergence of Lanczos eigenvalues for symmetric matrices

Consider the largest eigenvalue of a symmetric matrix. It satisfies:

$${\lambda }_1=\underset{x\ne 0}{\max }\frac{{\mathbf{x}}^{T}A\mathbf{x}}{\Vert \mathbf{x}{\Vert }_2^2}$$

The Lanczos approximation uses Ritz eigenvalues (see also Arnoldi process):

$$T_k=Q_k^{T}A{Q}_k$$

From

$${\lambda }_1(T_k)=\underset{y\ne 0}{\max }\frac{{\mathbf{y}}^T{Q}_k^{T}A{Q}_k\mathbf{y}}{\Vert \mathbf{y}{\Vert }_2^2}$$

we immediately find that ${\lambda }_1(T_k)\le {\lambda }_1$.

We can do a more precise analysis using polynomials again. Here is a brief outline. We have, using the polynomial interpretation of Lanczos and Krylov subspaces:

$${\lambda }_1(T_k)=\underset{p}{\max }\frac{{\mathbf{q}}_1^{T}p(A{)}^{T}Ap(A){\mathbf{q}}_1}{{\mathbf{q}}_1^{T}p(A{)}^2{\mathbf{q}}_1}$$

where $p$ is a polynomial of degree $k-1$.

By making the special choice of Chebyshev polynomials, we can prove that:

$${\lambda }_1\ge {\lambda }_1(T_k)\ge {\lambda }_1-({\lambda }_1-{\lambda }_n)(\frac{\tan \varphi }{T_{k-1}^{\mathrm{cheb}}(1+2{\rho }_1)}{)}^2$$

where $\varphi$ depends on $q_1$. We defined

$${\rho }_1=\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_2-{\lambda }_n}$$

Here is a schematic of the distribution of eigenvalues along the real axis for symmetric matrices:

With Chebyshev polynomials, we have

$$T_{k-1}^{\mathrm{cheb}}(1+2{\rho }_1)=O[(4{\rho }_1{)}^k]$$

We obtain a rapid convergence when ${\lambda }_1$ is well separated from the other eigenvalues and ${\rho }_1\gg 1$.

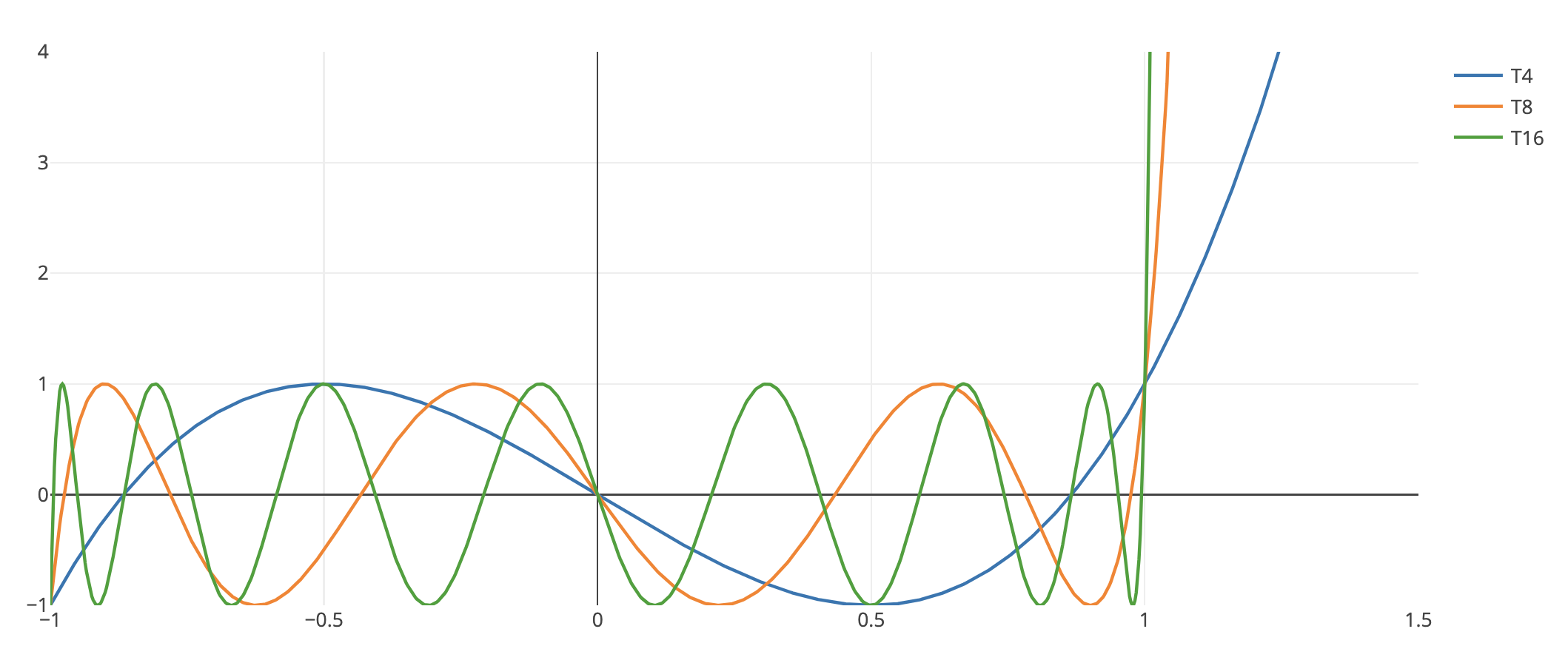
$T_{k-1}^{\mathrm{cheb}}(1+2{\rho }_1)$ becomes very large with $k$ quickly.