Orthogonal matrix and projector

A matrix $Q\in {\mathbb{R}}^{m\times n}$ is orthogonal if

$$Q^{T}Q=I$$

This means that the columns of $Q$ are orthogonal to each other.

Notation: ${}^H$ : transpose conjugate

Unitary: same for complex matrices: $Q^{H}Q=I$.

Orthogonal matrices are very important in numerical linear algebra. They often guarantee that an algorithm will be accurate.

Orthogonal matrices are isometries, that is, they conserve the 2-norm of a vector:

$$\Vert Qx{\Vert }_2=\Vert x{\Vert }_2$$

If $Q$ is square, then its inverse is $Q^T$.

Consider a unit vector $u$ then the square matrix

$$Q=I-2u{u}^T$$

is orthogonal and is a reflection matrix. It satisfies: $Q^T=Q^{-1}=Q$ and $Q^2=I$.

Cartan–Dieudonné theorem: Every square orthogonal transformation in ${\mathbb{R}}^n$ can be described as the composition of at most $n$ reflections: $Q=H_1\cdots H_k$, where $0\le k\le n$. If $k=0$, $Q$ is the identity matrix.

Proof: this is a proof by induction. If $n=1$, $Q$ is either 1 (identity) or $-1$ (reflection). Let’s assume that the theorem is true for $n-1$. Consider the canonical basis $e_1$, …, $e_n$. Define $z=Q{e}_n$. We can build a reflection $H$ (perhaps equal to the identity) such that $HQ{e}_n=e_n$. $HQ$ is square orthogonal:

$$(HQ{)}^T(HQ)=Q^T{H}^{T}HQ=Q^{T}Q=I$$

Moreover matrix $HQ$ has the form

$$HQ=\left[\begin{array}{cc}{Q}_{n-1}& 0\\ 0& 1\end{array}\right]$$

The last row must have zeros otherwise $HQ$ cannot be orthogonal. By induction, the matrix $Q_{n-1}$ is orthogonal and can be written as a product of at most $n-1$ reflections. Since $H$ is a reflection, $Q$ can be written as a product of at most $n$ reflections.

$\square$

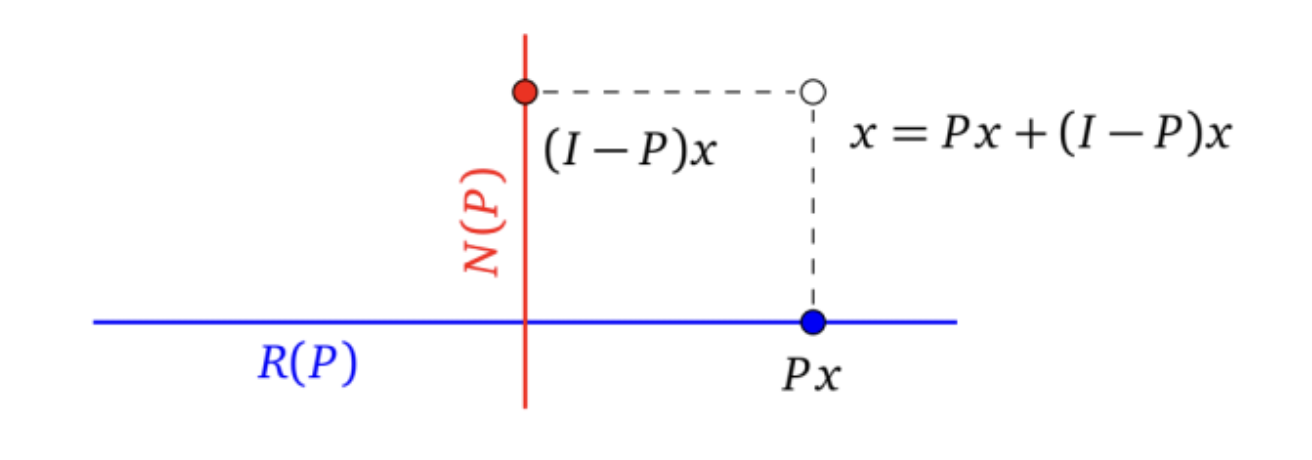
The matrix $Q{Q}^T$ is not equal to $I$ if $Q$ is rectangular (i.e., $m>n$).

The matrix $P=Q{Q}^T$ represents an orthogonal projection onto $R(Q)$ along $N(Q^T)$.

Dot product, Vector norms, Operator and matrix norms, Projection