Forward and backward error

Consider as an example problem solving $Ax=b$. We can think of the solution process as a map f: $(A,b)\mapsto x$.

Forward and backward error analysis can be formulated abstractly by representing any algorithm as a function $f$ that maps inputs to outputs.

Forward error equation: “What is the error in the solution computed with our algorithm?”

This corresponds to establishing bounds of the form:

$$\Vert \tilde{f}(A,b)-f(A,b)\Vert \le \dots$$

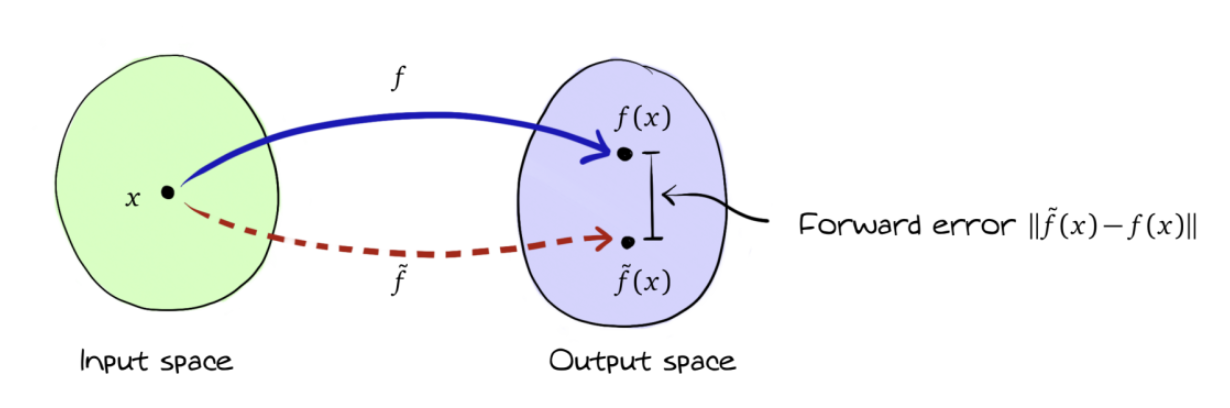
This is a natural question. However, a direct forward error analysis is difficult. In many numerical algorithms, a backward error analysis is much more useful.

Backward error equation: “What is the problem that our algorithm actually (exactly) solved?”

This corresponds to:

$$\tilde{f}(A,b)=f(\tilde{A},\tilde{b})$$

We now look for bounds of the type

$$\Vert A-\tilde{A}\Vert \le \dots ,\Vert b-\tilde{b}\Vert \le \dots$$

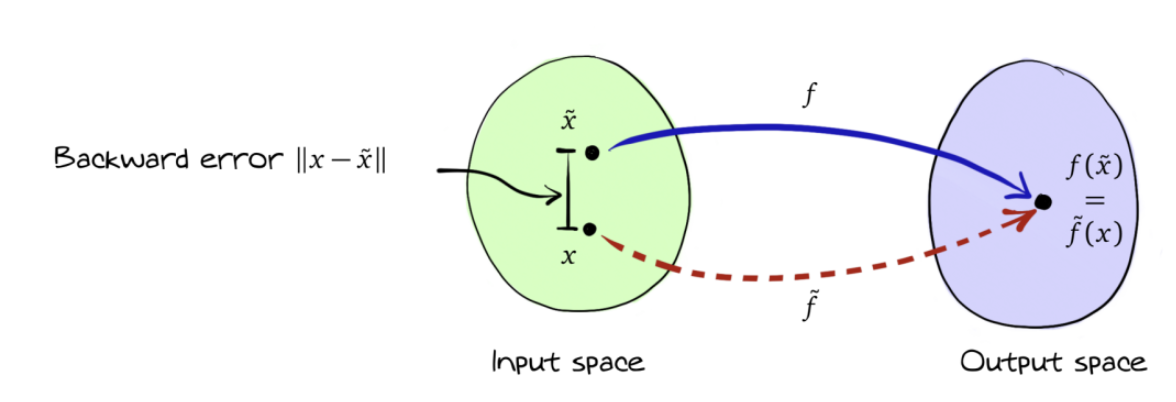
The forward error can be connected to the backward error using the conditioning of the problem.

Stability of the LU factorization, Floating point numbers, Floating point arithmetic and unit roundoff error