QR using Givens transformations

Summary

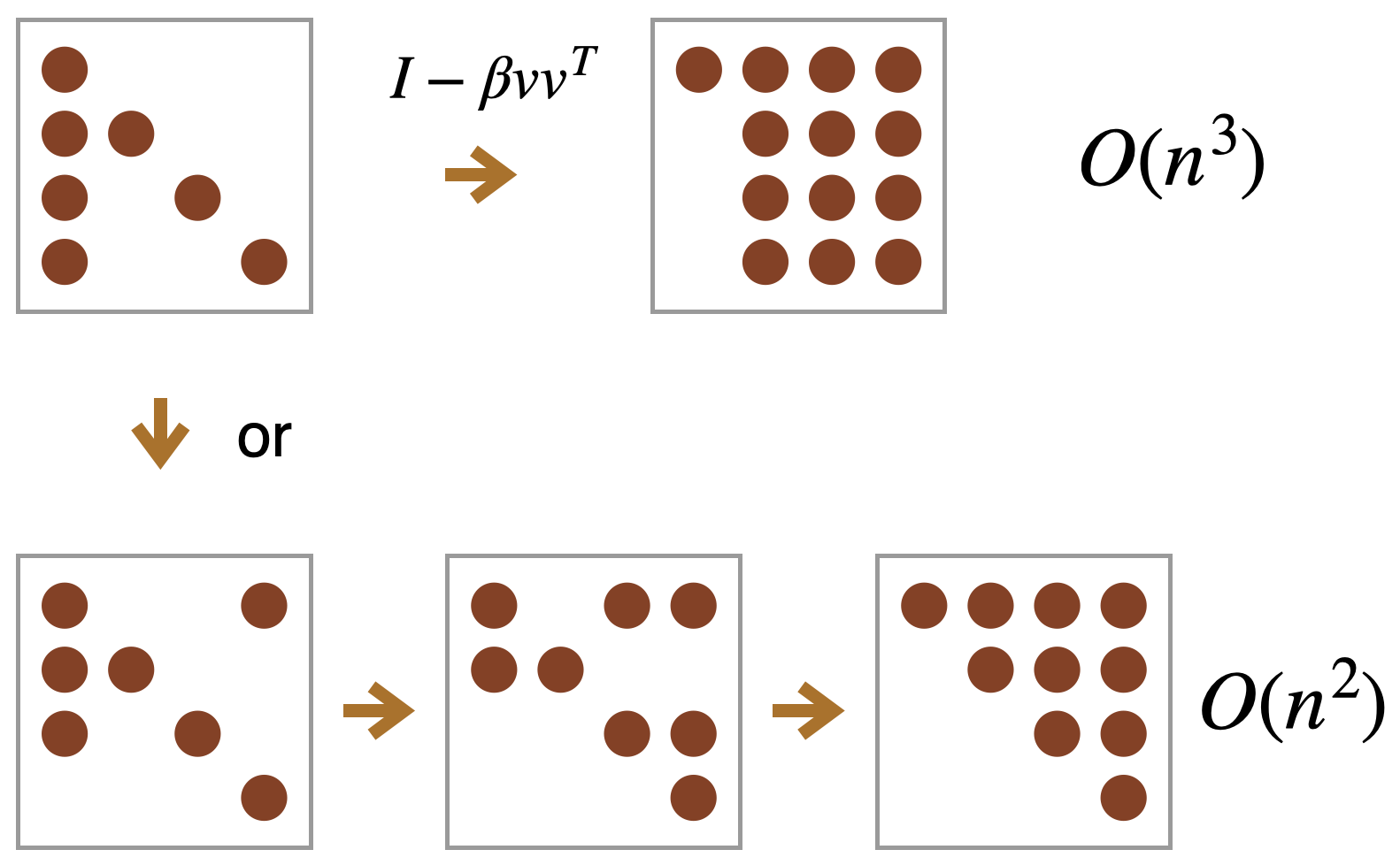
Householder Transformations

• Purpose: Transform an entire column of a matrix to align with a standard basis vector (usually $e_1$) in a single step.
• Approach: Use one large orthogonal matrix (Householder reflector) that operates on the whole column.
• Efficiency: Highly efficient for dense matrices because it reduces multiple elements to zero simultaneously.
• Computational cost: For an $m\times n$ dense matrix, the cost is $O(m{n}^2)$.

Givens Transformations

• Purpose: Zero out individual elements in a matrix while preserving orthogonality.
• Approach: Apply a sequence of small $2\times 2$ orthogonal matrices (Givens rotations or reflections) targeting specific entries.
• Efficiency:
  • Sparse matrices: More efficient than Householder transformations when dealing with sparse matrices like tridiagonal or upper Hessenberg matrices.
  • Single entry modification: Ideal for zeroing out individual elements without affecting the entire column.
• Computational cost: $O(m{n}^2)$ (slightly higher constant factor than Householder due to processing elements individually).

Example

Givens transformations will be very useful when dealing with Upper Hessenberg matrices (matrices that are zero below the sub-diagonal, i.e., $i>j+1$ implies that $a_{ij}=0$) and tri-diagonal matrices.

• Left figure: upper Hessenberg
• Right figure: tri-diagonal matrix.

2 approaches:

• Householder: one big Q transform. Fastest for dense matrices.
• Givens: many small $2\times 2$ Q transforms. Slower for dense matrices but faster for sparse matrices and for processing a single entry at a time.

Let’s go through some specific steps in this method.

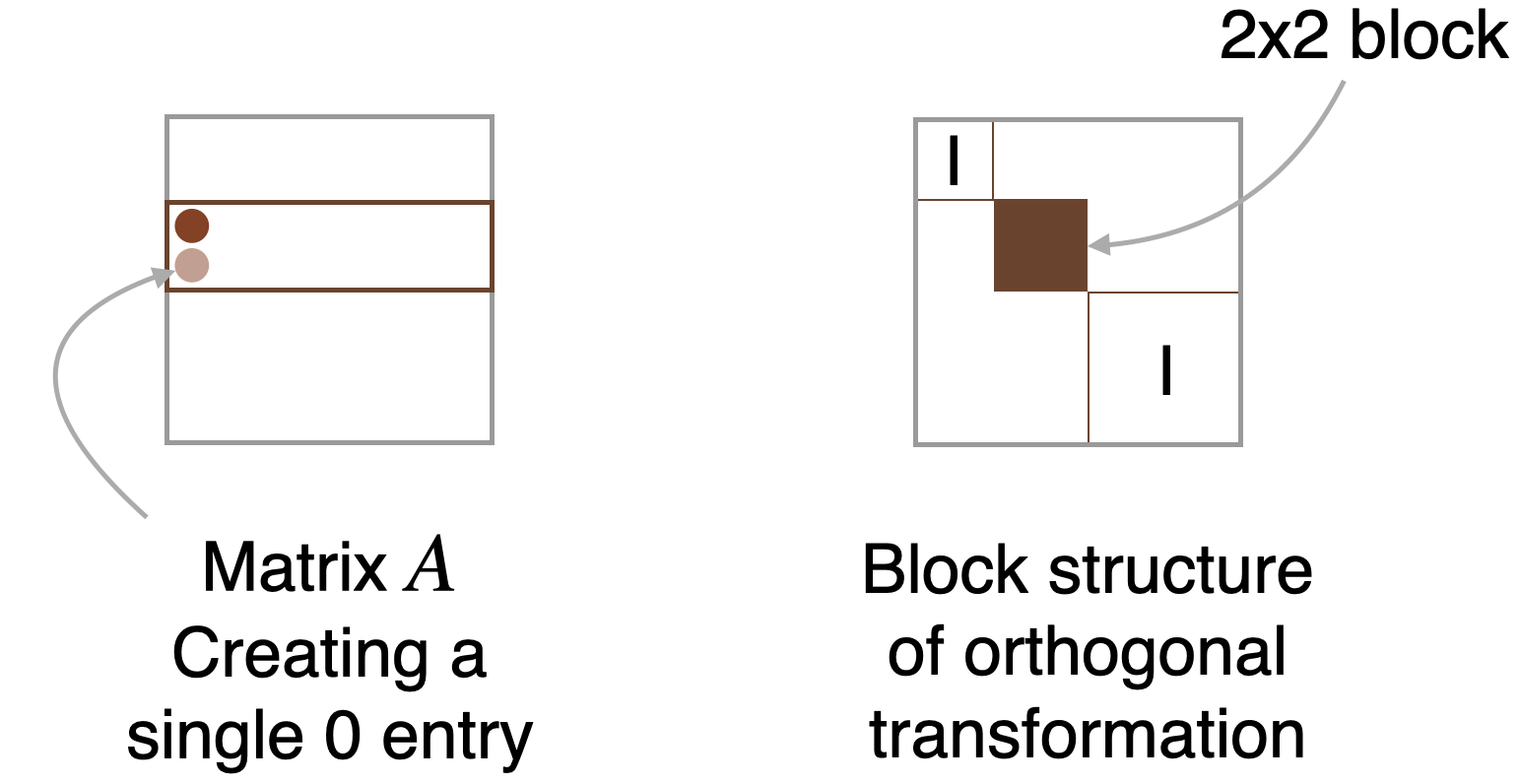
Take a vector $r$ of size 2:

$$r=\left(\begin{array}{c}x\\ y\end{array}\right)$$

Assume that these are the entries we want to modify. We want to zero out the 2nd entry using an orthogonal transformation.

Denote by:

$$c=\frac{x}{\Vert r{\Vert }_2},s=\frac{y}{\Vert r{\Vert }_2}$$

• We have two options for the $2\times 2$ orthogonal transformation.
• It can be a rotation or a reflection.
• There is no significant difference between these 2 options.

Rotation: det $=1$

$$\left(\begin{array}{cc}c& s\\ -s& c\end{array}\right)$$

Reflection: det $=-1$

$$\left(\begin{array}{cc}c& s\\ s& -c\end{array}\right)$$

You can check that this works:

$$\left(\begin{array}{cc}c& s\\ -s& c\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{cc}c& s\\ s& -c\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}\Vert r{\Vert }_2\\ 0\end{array}\right)$$

Let’s apply this method to our example:

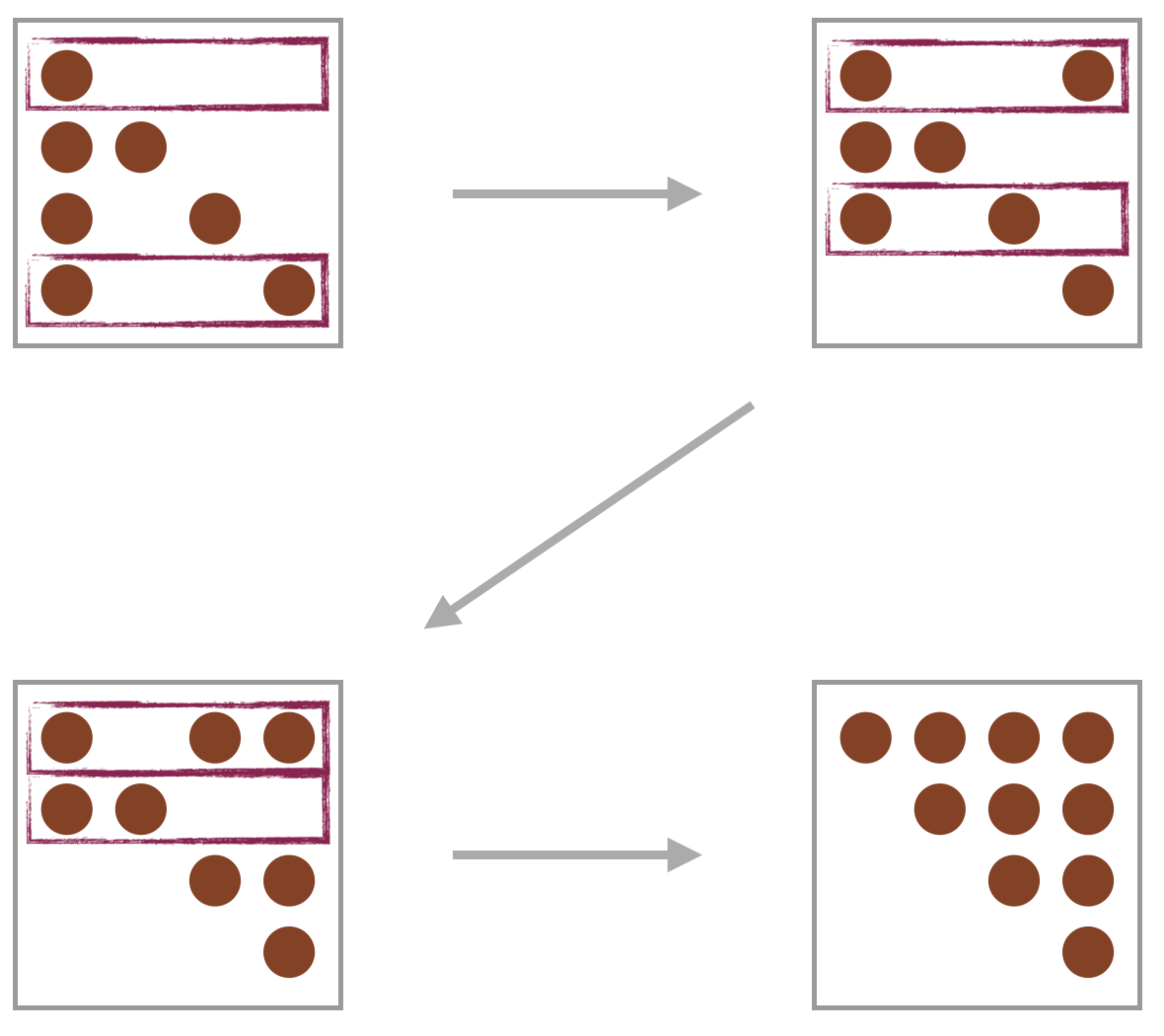
We get the matrix in the desired upper triangular form.

Computational cost

The computational cost of zeroing out a single entry is $O(n)$. So the cost for a single column is $O(n^2)$. The total computational cost for the entire matrix is $O(n^3)$.

• If matrix $A$ is a general $m\times n$ matrix, the cost is $O(m{n}^2)$.
• If $A$ is tri-diagonal, the cost is $O(\min (m,n))$.
• If $A$ is upper-Hessenberg, the cost is $O(mn)$.

QR factorization, Householder transformation, QR using Householder transformations