Householder transformation

QR factorization: $A=QR$

We can rewrite this equation as:

$$Q^{T}A=R$$

Interpretation: apply an orthogonal transformation to make the matrix triangular = orthogonal triangularization.

Start with 1st column.

$$a_{,1}\to \Vert a_{,1}{\Vert }_2{e}_1$$

• We need to apply an orthogonal transformation that zeros out all entries except the first.
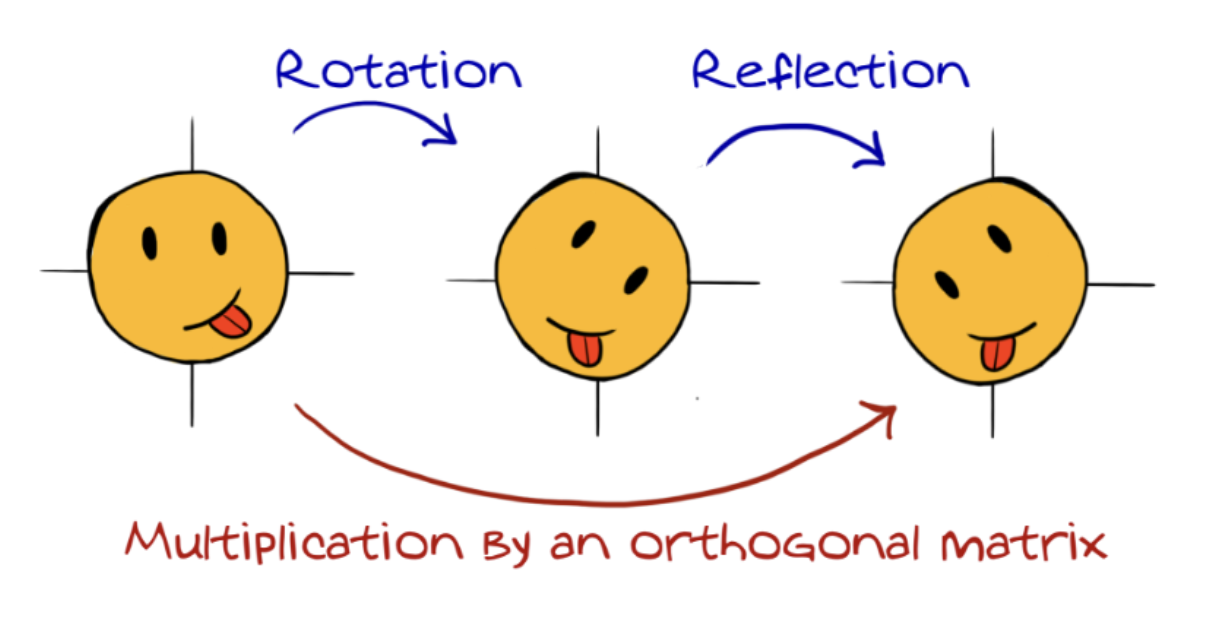
• Orthogonal transformations are either rotations or reflections.
• It turns out that reflections are easier to apply than rotations.

Orthogonal transformations are either rotations or reflections:

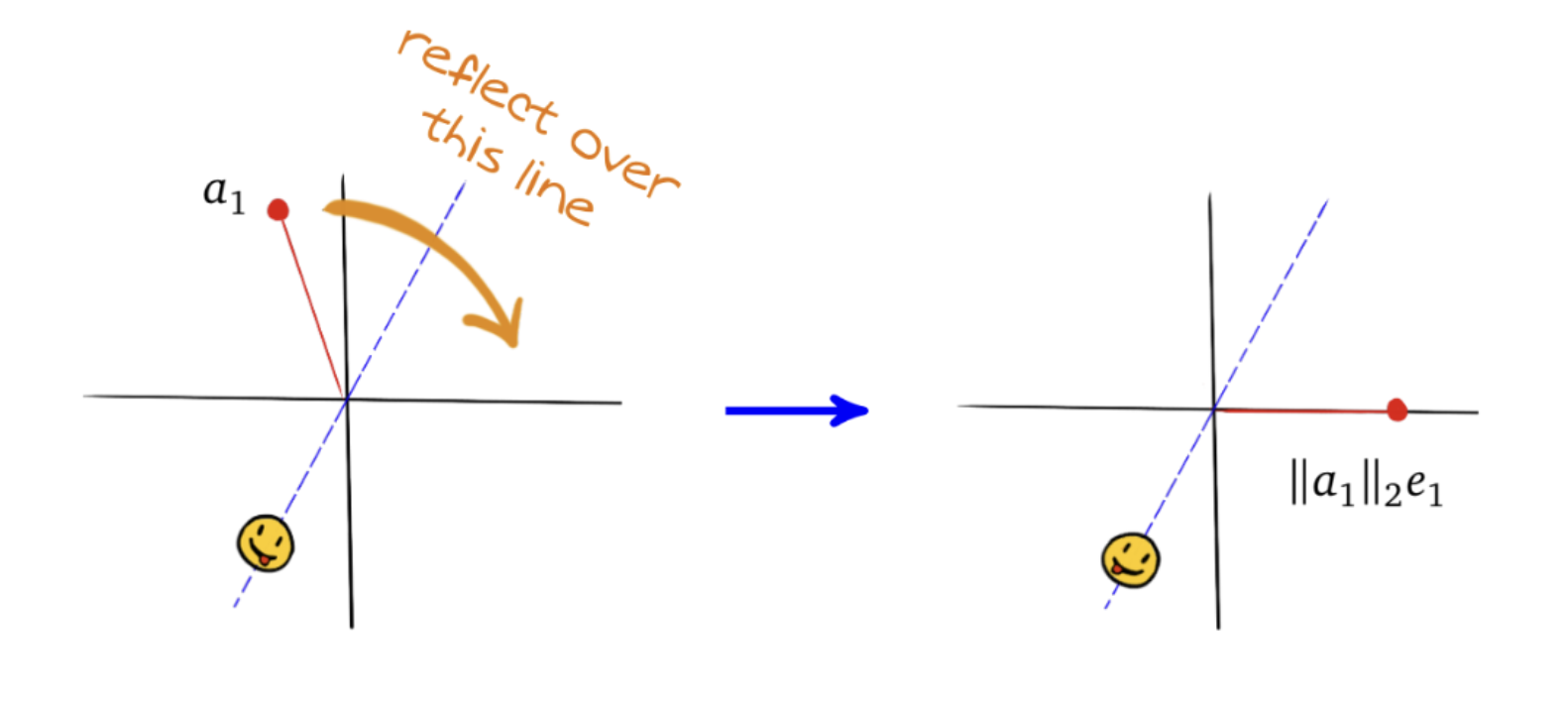
We want to find a reflection that sends the first column $a_{,1}$ to the $e_1$ axis:

These are the steps:

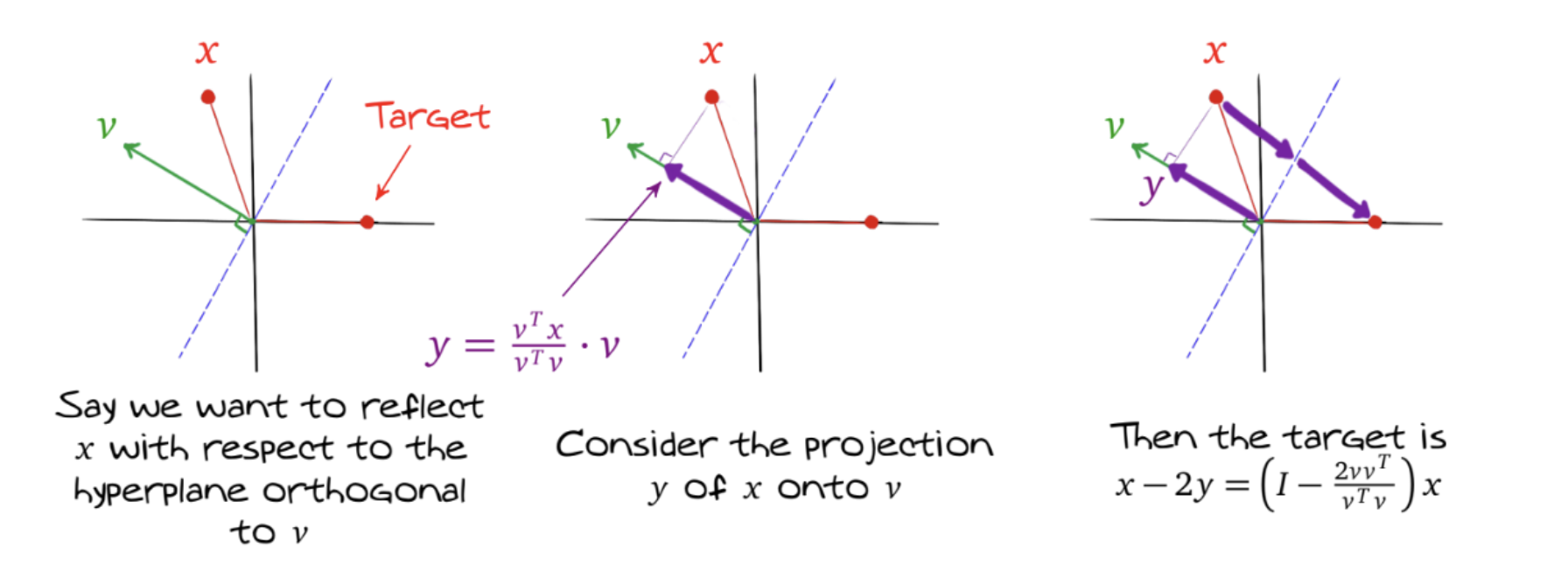
From this figure, we can derive the key definitions:

• Vector for projection: $v=x-\Vert x{\Vert }_2{e}_1$.
• Reflection matrix: $P=I-\beta v{v}^T$ with $\beta =\frac{2}{v^{T}v}.$

This completely defines the Householder transformation $P$.

Properties:

• We can check that $P^{T}P=I$. In fact: $P=P^T$ and $P^2=I$.
• We can check that $Px=\Vert x{\Vert }_2{e}_1$.

QR factorization